BOJ 2055 - 삼각형 찾기
| 시간 제한 | 메모리 제한 |
|---|---|
| 2 초 | 128 MB |
문제
삼각형이란 세 개의 변으로 이루어진 면적이 양수인 도형이다. 격자 삼각형이란 삼각형의 세 꼭짓점의 좌표가 정수로 표현되는 삼각형을 말한다. 격자의 범위가 N×M으로 주어질 때, 가능한 삼각형의 개수를 구하는 프로그램을 작성하시오. 예를 들어 N=1, M=2일 경우에는 다음과 같은 18개의 경우가 있다.
입력
첫째 줄에 두 정수 N, M이 주어진다.
출력
첫째 줄에 답을 출력한다.
제한
- 1 ≤ N, M ≤ 1,000
풀게 된 계기
- solved.ac에 삼각형을 검색한다.
- 뭔가 맛있어 보이는 이름이다.
- 뭔가 풀 수 있을 거 같은데 학원에서 수업은 듣기 싫으니까 풀어본다.
- 와 풀었어요..!!
풀이 과정
중학교나 고등학교에서 이런 문제는 한 번쯤 보신 적이 있을 겁니다.
이 문제를 푸는 방법은 다음과 같습니다.
- 전체 격자점 중 세 점을 고르는 경우의 수를 구한다.
- 세 점이 삼각형을 이루지 않는 경우를 전체 경우에서 뺀다.
여기서 세 점이 삼각형을 이루지 않는 경우는 세 점이 모두 일직선상에 있는 경우입니다.
이 경우에는 문제에서 가로와 세로 길이가 각각 4와 6으로 정해져 있었지만, 실제로 문제에서 요구하는 것은 임의의 가로와 세로 길이에 대한 해답입니다. 이것을 어떻게 구할 수 있을까요?
일단 문제에서는 점이 아니라 격자의 범위를 주었으므로, $N + 1$과 $M + 1$으로 점의 개수를 구할 수 있습니다. 또한, $N$과 $M$이 바뀌어도 답은 같기에 $N$과 $M$ 중에 작지 않은 값을 $X$, 다른 값을 $Y$라고 하겠습니다. 편의상 $X$를 가로 길이, $Y$를 세로 길이라고 하겠습니다.
일단 세 점이 모두 가로 또는 세로선에 평행한 경우는 쉽게 구할 수 있습니다. 각각 \((X+1) \cdot {}_{Y+1}C_3\), \((Y+1) \cdot {}_{X+1}C_3\)이 됩니다.
이제 다른 경우를 구해봅시다. 먼저 세 점을 각각 $P_1(a_1, b_1), P_2(a_2, b_2), P_3(a_3, b_3)$이라고 하겠습니다.
이때 이 세 점은 한 직선 위에 있습니다. 따라서 기울기가 같으며, 그 기울기를 $m$이라고 하면
\[\frac{b_2-b_1}{a_2-a_1} = \frac{b_3-b_2}{a_3-a_2} = \frac{b_3-b_1}{a_3-a_1} = m\]이 성립합니다.
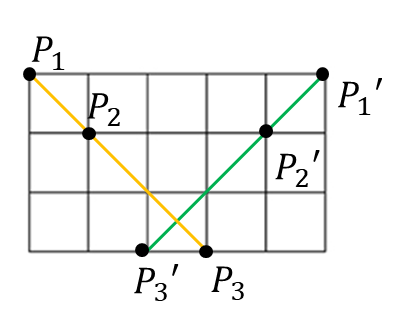
또한 세 점을 좌우 반전한 $P’_1(X - a_2, b_1), P’_2(X - a_2, b_2), P’_3(X - a_3, b_3)$ 역시 하나의 직선 위에 있는 점이 됩니다. 그림으로 나타내면 다음과 같습니다.
세 점이 같은 세로선에 있는 경우는 위에서 이미 세었기 때문에, 나머지 모든 점들의 쌍은 각각 세 점을 좌우반전한 점들의 쌍을 가집니다. 따라서, 둘 중에 기울기가 양수인 경우만 생각하고 구한 다음 2를 곱해주면 모든 일직선상에 있는 세 쌍의 점들의 개수를 구할 수 있습니다.
이제 이 세 점을 어떤 기준을 세워서 찾아야 할 것인데, 언제나 그렇듯 이때 중복이 발생하지 않도록 세는 것이 중요합니다.
위에서 세 점의 x,y좌표가 모두 다르다고 가정했습니다. 이때, $a_3 - a_1$은 세 점 중 x좌표가 가장 큰 것과 작은 것의 x좌표 차이라고 할 수 있습니다. 마찬가지로 $b_3 - b_1$은 y좌표의 차이가 됩니다. 이제 $a_3 - a_1 = w$, $b_3 - b_1 = h$라고 두겠습니다.
$w$와 $h$가 같은 직선상의 점 세 쌍은 가로가 $w$, 세로가 $h$인 직사각형 내의 직선상의 점 세 쌍으로 생각할 수 있습니다.
여기서 중요한 점은,
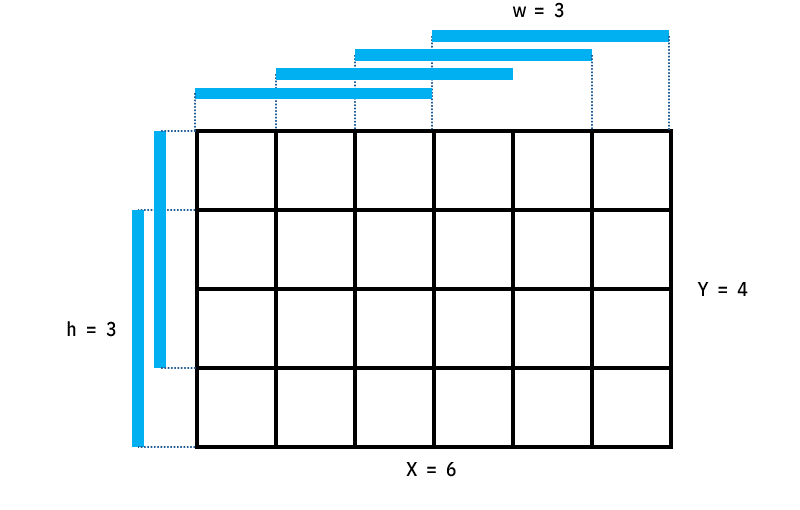
가로 길이가 $w$이고 세로 길이가 $h$인 직사각형은 전체 직사각형 (가로 $X$, 세로 $Y$)에 총 $(X-w+1)(Y-h+1)$개 있다.
라는 것입니다. 증명은… 어렵지 않지만 그림으로 대신하겠습니다.
이제 각각의 $w$와 $h$에 대하여 가능한 중간 지점, 즉 $B(a_2, b_2)$의 조합의 수를 구한 후 그 값을 $l$이라고 합시다. 그러면, 전체 직사각형에 포함되는 일직선상에 있는 세 점들의 쌍의 개수는 $2l \cdot (X-w+1)(Y-h+1)$이 됩니다. (좌우 대칭을 고려해야 함에 유의하세요!)
이때 $w$과 $h$는 모두 직사각형 내부의 점들로 이루어져 있으므로, $0 < w \leq X$이고 $0 < h \leq Y$인 $w$와 $h$들에 대해 가로 길이가 $w$, 세로 길이가 $h$인 세 점의 쌍의 개수를 조사해주면 됩니다.
결론부터 말하자면, 어떤 $w$와 $h$에 대해 가로 길이가 $w$, 세로 길이가 $h$인 세 점의 쌍의 개수는 $GCD(w, h) - 1$개입니다.
먼저 처음에 이야기하였듯, 이 세 점들의 기울기는 $\displaystyle \frac{b_2-b_1}{a_2-a_1} = \frac{b_3-b_1}{a_3-a_1} = \frac{h}{w} = m$이 됩니다.
따라서 어떤 유리수 $0 < t < 1$에 대해, $B(a_1 + wt, b_1 + ht)$로 나타낼 수 있습니다.
(이는 $B$가 $A$와 $C$의 내분점이라는 것으로도 해석할 수 있습니다.)
이제 두 자연수 $0 < p < q$에 대해 $t = \dfrac{p}{q}$로 나타낸다면, $B$ 역시 $B(a_1 + \dfrac{wp}{q}, b_1 + \dfrac{hp}{q})$로 나타낼 수 있습니다.
$B$ 점 역시 좌표가 정수여야 하기 때문에, $q \vert h$ 그리고 $q \vert w$여야 합니다. 따라서 $q$는 $h$와 $w$의 공약수입니다.
이때 이러한 $q$들 중 가장 큰 값을 $g$라고 한다면, $g = GCD(h, w)$인 것은 자명합니다.
그리고 $g$보다 작은 $q$는 $g$의 약수이므로, 어떤 $k$에 대해 $\dfrac{p}{q} = \dfrac{pk}{qk} = \dfrac{pk}{g}$로 나타낼 수 있습니다.
왜 $q$가 $g$의 약수인가요?
모든 공약수는 최대공약수의 약수이기 때문입니다.
그러니까, $0 < p < g$인 $\dfrac{p}{g}$의 개수가 $B$ 점의 개수가 되는 것입니다. 따라서 $p$는 $g-1$개 존재합니다.
여기서 $GCD(1, x)$는 항상 $1$이기 때문에, $w = 1$ 또는 $h = 1$인 경우는 무조건 $0$이 되는 것을 알 수 있습니다. 따라서 $2 \leq w \leq X$, $2 \leq h \leq Y$인 $w, h$에 대해서만 구해주어도 충분합니다.
우리가 구해야 할 것은 다음과 같습니다.
- 직사각형에서 고를 수 있는 모든 세 점의 쌍의 개수 = ${}_{(X+1)(Y+1)}C_3$
- 직사각형에서 같은 가로줄과 세로줄에 있는 점들의 개수 = \((X+1) \cdot {}_{Y+1}C_3 + (Y+1) \cdot {}_{X+1}C_3\)
- $2 \leq w \leq X, 2 \leq h \leq Y$인 모든 $(w, h)$에 대하여 $2 \cdot (X-w+1)(Y-h+1) \cdot GCD(w, h)$의 값을 구한다.
- 1에서 2와 3의 값을 빼주면 끝!
이때 $GCD(w, h)$의 수행 시간은 $O(\text{log }Y)$보다 작거나 같습니다. 따라서 이 풀이의 시간복잡도는 $O(XY\text{ log }Y)$가 됩니다. 문제에서 $N, M \leq 1,000$이라고 했으니 충분히 시간 내에 수행할 수 있습니다!
구현
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
using namespace std;
#include <bits/stdc++.h>
using i64 = long long;
inline i64 C3(i64 n) { // nC3 반환
return n * (n-1) / 2 * (n-2) / 3;
}
int main() {
int x, y;
cin >> x >> y;
if (x < y) swap(x, y); // 둘 중 긴 변이 x
i64 count = C3((x + 1) * (y + 1)); // 전체 세 점들의 쌍 개수
count -= (x + 1) * C3(y + 1); // 세로로 일직선에 놓인 쌍들의 수
count -= (y + 1) * C3(x + 1); // 가로로 일직선에 놓인 쌍들의 수
for (int h = 2; h <= y; h++) {
for (int w = 2; w <= x; w++) {
count -= 2 * (x - w + 1) * (y - h + 1) * (gcd(w, h) - 1); // 가로 길이가 w, 세로 길이가 h인 쌍들의 수
}
}
cout << count;
}
수의 범위가 32비트를 벗어나는 것에 유의하세요.
마치며
사실 제 첫 풀이는 이것과는 약간 다른 방식이었는데, 조금 더 복잡하고 약간의 비효율이 있어서 개선된 풀이로 설명하였습니다. 기본적인 아이디어는 같습니다.
이상하게 pypy를 쓰면 첫 풀이가 더 빠르게 돌더라고요. pypy로 돌리면 종종 상식과 어긋나는 실행속도가 나오는 경우가 꽤 있었습니다. 그만큼 최적화를 잘 해준다는 뜻이기도 하겠지만요.
그리고 이 문제를 ‘30분만에 풀었다’면서 주변 사람들에게 열심히 바이럴하고 다녔습니다. 지금도 열심히 푸는 분들이 계시는 걸 보면 기분이 좋아요(?)
바이럴한 데애 대한 책임은 져야 할 거 같아서 이렇게 글도 쓰게 되었고요. 재미있는 문제였습니다!