BOJ 1353 - 합과 곱
| 시간 제한 | 메모리 제한 |
|---|---|
| 2 초 | 128 MB |
문제
음이 아닌 수의 리스트가 있을 때, 그 리스트에 있는 수의 합이 S이고, 곱이 P일 때, 만족하는 리스트라고 한다.
S와 P가 주어졌을 때, 가능한 만족하는 리스트의 크기중 최소를 출력한다. 리스트의 크기란 그 리스트에 있는 수의 개수를 말한다. 만약 그러한 것이 없다면 -1을 출력한다.
리스트에는 정수가 아닌 수가 포함될 수도 있다.
입력
첫째 줄에 S와 P가 주어진다. S와 P는 1,000,000,000보다 작거나 같은 자연수이다.
출력
첫째 줄에 정답을 출력한다.
풀게 된 계기
이 문제를 풀 때까지만 해도 PS에 이렇게 깊이 빠질 줄은 몰랐습니다.
아니, 사실상 이 문제 때문에 PS에 빠지게 되었다 해도 과언이 아닐 것 같습니다.
저는 개인 Discord 서버에서 다른 분들이 BOJ 문제를 풀고 계시는 걸 보고 “나도 잠깐 찍먹이나 해 볼까?” 하는 생각이 들어 문제들을 몇 개 풀고 있었습니다. 그리고 문제의 저 채팅이 등장합니다.
플래… 멋있잖아요?
바로 풀러 달려갔습니다.
풀이 과정
일단 리스트의 크기를 n이라고 할 때, 리스트의 원소들을 $a_1, a_2, …, a_n$으로 나타낼 수 있습니다.
문제의 조건에 따라 우리가 구해야 할 것은
$\displaystyle S = a_1 + a_2 + … + a_n = \sum_{k=1}^n a_k$
$\displaystyle P = a_1 a_2 … a_n = \prod_{k=1}^n a_k$
를 만족하는 $a_n$의 리스트, 그 중에서도 길이가 가장 짧은 리스트가 됩니다. 여기서 떠오른 것이 바로 산술-기하 평균 부등식이었습니다. 산술-기하 평균 부등식은 다음의 절대부등식을 의미하며, 고등학교 교육과정에서도 배우는 내용입니다.
$\displaystyle \frac{a_1 + a_2 + … + a_n}{n} \geq \sqrt[^n]{a_1 a_2 … a_n}$
또한 $a_1 = a_2 = … = a_n$일 때 등식이 성립하는 것으로 알려져 있습니다.
위의 부등식에 따라 식을 정리해 보면, $\displaystyle \frac{S}{n} \geq \sqrt[^n]{P}$ 를 만족하는 n을 찾아야 하는 것임을 알 수 있습니다. 미지수 n이 양 변에 있으므로 양 변을 n제곱해줍니다. (S와 P는 모두 음수가 아니기에 가능합니다.) 그럼 $\displaystyle (\frac{S}{n})^n \geq P$으로 식이 변형되는데, 우리는 이제 S와 P를 모두 알고 있기 때문에 저 식은 오로지 미지수 n에 관한 부등식입니다!
…그래서 이제 저걸 어떻게 풀죠?
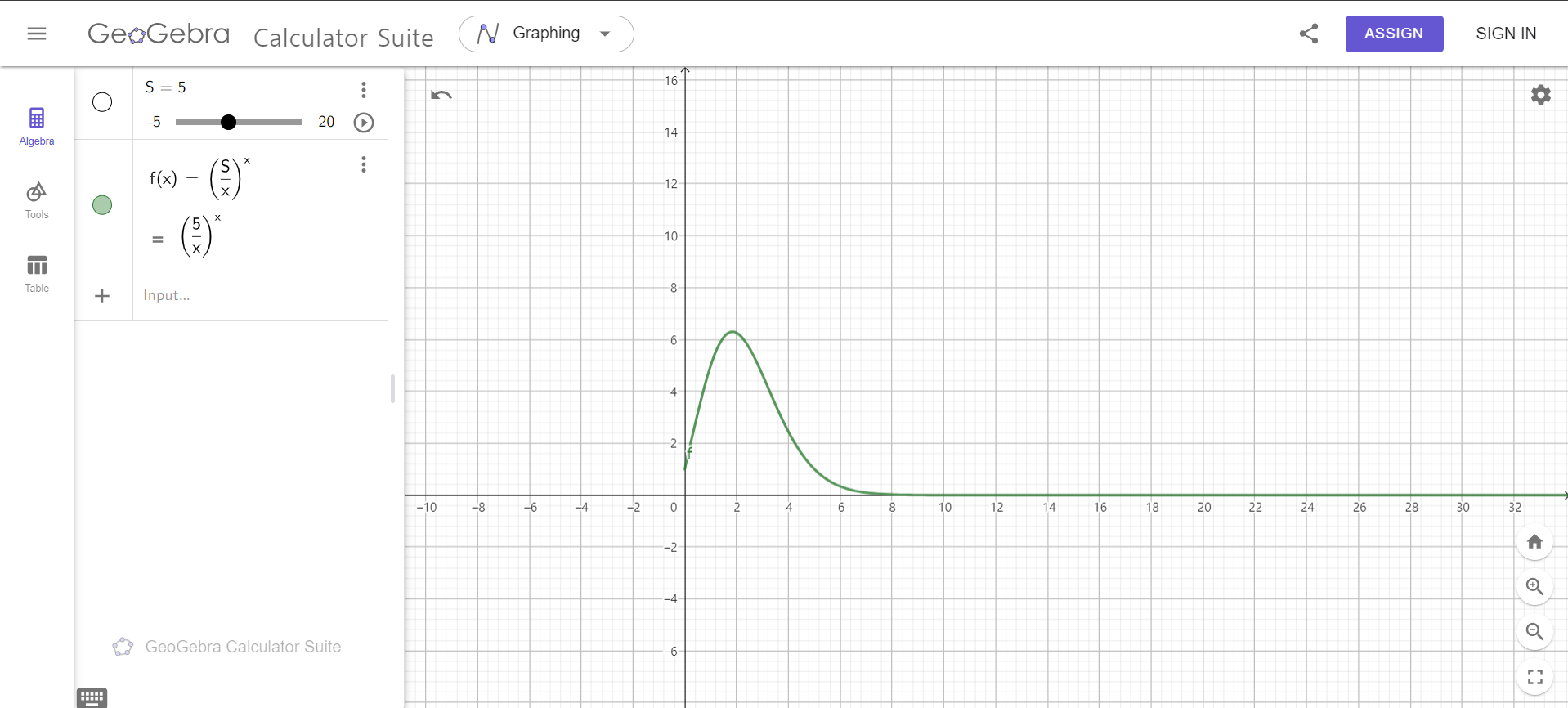
좋아요, 지오지브라는 신이며 이는 고구려 수박도에도 나와 있습니다.
사실 $f(n) = (\frac{S}{n})^n$으로 두고 양변에 로그를 취한 후 미분하는 등의 과정을 거치는 게 정석적인 방법이 아닐까 싶습니다. 이 풀이도 아래에 나와있어요.
아무튼, 이제 개형을 알았으니 우리가 해야 할 것은, 그냥 f(n)에 1부터 값을 쭉 대입해보다가, 극대점을 지나면 종료하는 겁니다. 조금 짜치지만(?) 대충 값을 대입하다 보면, 극대점의 x좌표가 선형 탐색으로 충분히 탐색할만한 범위 내라는 것은 금방 알 수 있습니다.
오, 완벽한 풀이야..! 하고 구현했습니다. 계산 과정에서 숫자가 굉장히 커져서 C#의 BigInteger도 사용했고요. C#이 확실히 이런 면에서는 편한 부분이 있습니다. 그리고…
사소한 문제들이 많이 있었지만, 좀 더 중대한 문제도 있었습니다. 대표적으로 S = 1, S = 2인 경우가 있었는데, 이 경우 극대점의 x좌표가 1보다 작아집니다. 그래서 이 경우는 가능한 모든 경우 ((S = 1, P = 1), (S = 2, P = 1), (S = 2, P = 2))인 경우에 대해 조건 분기로 따로 처리해주었습니다.
그리고…
맞았습니다!
미분해서 극대점 구하기
$\displaystyle f(n) = (\frac{S}{n})^n$ 의 양 변에 로그를 취해 $\displaystyle ln\ f(n) = n(ln\frac{S}{n})$로 만들고, n에 대해 미분해주면 $\displaystyle\frac{f’(n)}{f(n)} = ln\frac{S}{n} - 1$이 되어, $\displaystyle f’(n) = (\frac{S}{n})^n (ln\frac{S}{n} - 1)$이 됩니다. 극대점에서 $f’(n) = 0$이고, $\displaystyle(\frac{S}{n})^n > 0$이므로 $\displaystyle ln\ \frac{S}{n} = 1$인 n에서 극대를 가집니다. 이러한 n을 구하면 $n = e \cdot S$가 되는데, 이때 주의해야 할 것은 $e \cdot S$를 올림한 점까지 구해보아야 한다는 것입니다. 왜냐하면 극대점 오른쪽의 정수점에서 $f(n)$의 함숫값이 최대를 가질 수도 있기 때문이죠. 어떻게 구하든 풀이는 같습니다.
여하튼, 재미있게 푼 문제였고 푼 이후에도 탐구를 조금 더 이어나갔었는데, 이에 대한 내용은 언젠가 생각이 난다면 적어보도록 하겠습니다.