OMCB014
nflight11님이 tester로 참여하셨다는 OMCB014에 참가해 보았습니다. 사실 전에 OMCB013도 참가해 보았어요.
스터디 카페에서 풀까, 아니면 집에서 풀까 고민하다 노트를 챙기지 않았다는 사실을 깨닫고 바로 집으로 달렸습니다.
A
$n\text{번째로 작은 소수} = 2n + 1$인 $n$의 값을 모두 더하여라.
소수들을 나열해 보면 $n = 2, 3, 4$만이 가능하다는 것을 쉽게 알 수 있습니다.
그 와중에 저는 $3 + 5 + 7 = 15$를 제출했다가 1틀을 적립했어요;
B
$a + b + c = 101$을 만족하는 양의 홀수 쌍 $(a, b, c)$는 모두 몇 개인가?
$a = 2a’ - 1, b = 2b’ - 1, c = 2c’ - 1$로 두고 풀면 $a’ + b’ + c’ = 52$가 됩니다. 직접 세어 보면 답은 $1275$가 됩니다.
에디토리얼에서는 $a = 2a’ + 1$, … 로 두고 $a’ + b’ + c’ = 49$, \({}_{49+2}\text{C}_{2}\)를 구하는 더 세련된 방식을 사용했더라고요. 이것도 알아두면 좋겠다 싶었습니다.
C
OMC 군은 하나의 자연수를 생각하고 있다. 당신은 OMC에게 자연수 $a, b$에 대해 다음과 같은 계산을 하도록 지시한다.
- 생각한 수를 10배 한 후 a를 더하고, 그 값을 11배 한 후 다시 b를 빼고, 다시 a로 나눈 후 처음 생각한 수를 뺀다. 이때 최종 계산 결과는 OMC 군이 처음에 생각한 수와 관계없이 11이다. $a + b$의 값을 구하라.
처음 생각한 수를 $x$라고 하면, 주어진 식은 $\dfrac{11(10x + a) - b}{a} - x = 11$이 됩니다. x에 대해 정리해 주면, $(110-a)x = b - 10a$가 됩니다. 이 식이 $x$에 대한 항등식이므로, $a = 110$, $b = 10a = 1100$이 되어 답은 $1210$입니다.
D
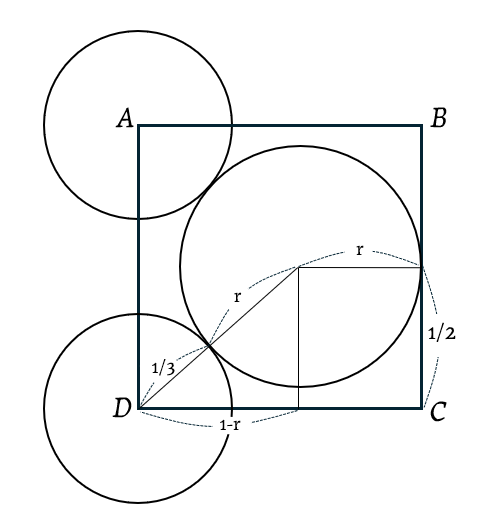
한 변의 길이가 $1$인 정사각형 $ABCD$에 대해 점 $A, D$를 각각 중심으로 하는 반지름이 $\dfrac{1}{3}$인 2개의 원을 생각하자. 이 2개의 원에 외접하고 변 BC와도 접하는 원의 반지름을 구하라. 답이 서로소인 두 자연수 a, b에 대해 $\dfrac{a}{b}$일 때, $a+b$의 값을 답하여라.
번역기에 넣을 때 반지름을 $1$로 넣어버리는 바람에, 6틀(…)이라는 뻘짓을 했던 문제입니다.
대충 이런 식으로 피타고라스 정리를 이용해 풀었습니다.
E
$\displaystyle \lfloor \frac{10^n}{m} \rfloor = 2024$인 두 자연수 쌍 $(m, n)$에 대해, $m$의 최솟값을 구하라.
$10^n = 2024 \cdot m + r \ \ (0 \leq r < m)$인 정수 $m$과 $r$을 찾아 풀었습니다.
식을 다시 정리해주면 $10^n - 2024 \cdot m = r < m$이 됩니다. 그리고 $m$을 일종의 손 이분탐색(?) 해 가면서 $4$ -> $49$ -> $494$까지 했을 때, $10^7 - 2024 \cdot 494 < 494$더라고요. 그래서 답 $494$를 찾았습니다.
에디토리얼을 보니, $\dfrac{1}{2025} < \dfrac{m}{10^n} \leq \dfrac{1}{2024}$ 이렇게 풀었더라고요. 제가 너무 멍청하게 구했다는 생각이 들었습니다.
사실 E번을 F번 푼 다음에 풀었습니다.
F
수열 ${a_n}$을 다음과 같이 정의하자. $a_1 = a_2 = 1, a_{n+2} = max(a_n + a_{n+1}, a_n a_{n+1})$ 이때, 양의 약수의 개수가 $5040$개인 $a_k$ 항이 단 하나 존재한다. 이 $a_k$는 두 소수 $p, q$와 자연수 $a, b$에 대해 $p^a q^b$ 꼴로 타낼 수 있다. 이때 $abqp$를 답하여라.
$a_k$와 $a_k+1$ 중 하나가 $1$이 아니라면 $a_{k+2}$는 항상 $a_k a_{k+1}$이 됩니다. 직접 수열을 구해 보면 $a_3$부터 $a_k = 2^{F_{k-4}} 3^{F_{k-3}}$으로 나타난다. ($F_n$은 피보나치 수열)
$a_k$의 약수의 개수는 $(F_{k-4}+1)(F_{k-3}+1)$이고, 피보나치 수열을 쭉 나열해 보면 $(55 + 1)(89 + 1) = 5040$임을 알 수 있습니다. 따라서 답은 $2 \cdot 55 \cdot 3 \cdot 89 = 29370$.
G
각 자리 수가 모두 다르고, 0을 포함하지 않는 3자리의 자연수 $N$이 있다. 이 $N$의 자릿수를 재배열한 $6$개의 자연수 ($N$ 포함)은 모두 $m$의 배수이다. $m$이 될 수 있는 모든 자연수의 합을 구하라.
각 자리 수를 $a$, $b$, $c$라고 하자. 이때 $N = 100a + 10b + c$가 된다. 이제 십의 자릿수와 일의 자릿수를 바꾼 수를 원래 수에서 빼면, $9(b - c)$가 되고 이 수는 $m$으로 나누어떨어져야 합니다. 백의 자릿수와 일의 자릿수를 바꾸면 $99(a - c)$가 되며, 이 수 역시 $m$으로 나누어떨어져야 합니다. 위 두 식은 $a, b, c$의 쌍 각각 모두에 성립해야 합니다.
먼저 $m = 1$인 경우는 항상 성립합니다. 또한 $m = 3, m = 9$인 경우는 $369$로 $9$의 배수 판정법에 따라 자명합니다. 이제 $m \not = 9$인 경우를 생각해 보면, $a - b, a - c, b - c$ 모두 $m$의 배수여야 합니다. 따라서 $a, b, c$의 차가 $m$의 배수여야 합니다.
먼저 $m = 2$인 경우는 $a, b, c ∈ {2, 4, 6, 8}$이 됩니다. 이때 가능한 $m$은 $m = 2, m = 2 \cdot 3, m = 2 \cdot 9$입니다. 그러나 $a - b, a - c, b - c$가 $m$으로 나누어떨어져도 $N$ 자체가 $m$으로 나누어떨어지지 않을 수 있기 때문에 모든 경우를 생각해 보면, $N = 468$일 때 $m = 2, m = 6, m = 18$인 경우를 모두 만족하는 것을 알 수 있습니다.
$m = 3$인 경우도 마찬가지로 구해 준다면 $a, b, c ∈ {3, 6, 9}$입니다. 이때 가능한 $m$은 $m = 3 \cdot 3, m = 3 \cdot 9$인데, $m = 9$인 경우는 이미 확인했으니 $m = 27$만 확인하면 됩니다. 그러나 $369$는 $27$로 나누어떨어지지 않아 $m$은 $27$이 될 수 없습니다.
따라서 가능한 $m$은 $1, 2, 3, 6, 9, 18$이 되어 답은 $39$가 됩니다.
처음에는 $27$도 되는 줄 알고 1틀, 그리고 덧셈을 잘못해서 2틀을 내 버렸다고 합니다.
H
원 $Γ$ 에 내접하는 볼록 오각형 $ABCDE$ 는 다음 조건을 만족한다. $AB=CD=EA=2,BC=DE=3$ $Γ$의 면적을 구하라. 이때, 구하는 면적은 서로소인 두 정수 $a, b$에 대해 $\dfrac{a}{b}π$ 로 나타낼 수 있으므로, $a + b$를 답하여라.
못 풀었습니다.
나중에 에디토리얼 보고 풀이라도 올려 보겠습니다.
총평
154/303등을 했습니다. 시험기간이라 그런지 정신이 메롱하네요
번역기 이슈도 있었고…
그래도 문제 푸는 건 재밌었으니 만족합니다!